Thursday, March 30, 2006
Wednesday, March 29, 2006
Paradoxo de Russell
Em 1901, Russell tomou conhecimento do trabalho desenvolvido por Frege em "Grundgesetze der Arithmetik". Mas apenas em 1902 teve oportunidade de o analisar detalhadamente e de "fazer um estudo mais rigoroso", como refere na carta que mais tarde enviou a Gottlob Frege. Nesta obra, Frege tentava reduzir a aritmética à lógica e Russell, ao analisá-la, descobre uma contradição no sistema proposto. Como escreve:
"Há apenas um ponto onde encontrei uma dificuldade. O colega diz que uma função também pode actuar como elemento indeterminado. Eu acreditava nisto, mas agora esta perspectiva parece-me duvidosa pela seguinte contradição. Seja w o predicado: para ser predicado, não pode ser predicado de si próprio. Pode w ser predicado de si próprio?"
[Carta enviada por Russell a Frege, 16 de Junho de 1902]
Usando linguagem matemática actual, o paradoxo toma a seguinte forma:
Considere-se o conjunto M como sendo "o conjunto de todos os conjuntos que não se contêm a si próprios como membros". Formalmente: A é elemento de M se e só se A não é elemento de A.
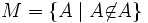
Será que M se contém a si mesmo? Se sim, não é membro de M de acordo com a definição.Por outro lado, supondo que M não se contém a si mesmo, tem de ser membro de M, de acordo com a definição de M. Assim, as afirmações "M é membro de M" e "M não é membro de M" conduzem ambas a contradições.
Após ter descoberto o paradoxo, Russell decide comunicar a Frege o sucedido através de uma carta. Quando recebeu a dita carta, o seguundo volume dos Grundgesetze estava quase a ser publicado. Frege viu, desse modo, grande parte do seu trabalho perdido. Consciente das dificuldades que o paradoxo lhe trazia, Frege acrescentou um apêndice ao livro como resposta a esta descoberta de Russell no qual não pode deixar de expressar uma enorme consternação:
"Um cientista dificilmente se pode deparar com algo tão indesejável como o de ver os fundamentos ruírem exactamente quando o seu trabalho está terminado. Fui colocado nesta posição por uma carta do Sr. Bertrand Russell, quando o trabalho já estava quase todo impresso."
Em resultado do paradoxo, Frege viu-se obrigado a abandonar muitos dos seus pontos de vista. Russell, que entretanto publica "The Principles of Mathematics", acrescenta também ao seu livro um apêndice onde explica em detalhe o paradoxo.
Este paradoxo possui uma versão mais popular intitulada O Paradoxo do Barbeiro.
O paradoxo considera uma aldeia onde um barbeiro faz a barba todos os dias a todos os hoomens que não se barbeiam a si próprios, e a mais ninguém. Ora tal aldeia não pode existir:
"Há apenas um ponto onde encontrei uma dificuldade. O colega diz que uma função também pode actuar como elemento indeterminado. Eu acreditava nisto, mas agora esta perspectiva parece-me duvidosa pela seguinte contradição. Seja w o predicado: para ser predicado, não pode ser predicado de si próprio. Pode w ser predicado de si próprio?"
[Carta enviada por Russell a Frege, 16 de Junho de 1902]
Usando linguagem matemática actual, o paradoxo toma a seguinte forma:
Considere-se o conjunto M como sendo "o conjunto de todos os conjuntos que não se contêm a si próprios como membros". Formalmente: A é elemento de M se e só se A não é elemento de A.
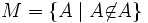
Será que M se contém a si mesmo? Se sim, não é membro de M de acordo com a definição.Por outro lado, supondo que M não se contém a si mesmo, tem de ser membro de M, de acordo com a definição de M. Assim, as afirmações "M é membro de M" e "M não é membro de M" conduzem ambas a contradições.
Após ter descoberto o paradoxo, Russell decide comunicar a Frege o sucedido através de uma carta. Quando recebeu a dita carta, o seguundo volume dos Grundgesetze estava quase a ser publicado. Frege viu, desse modo, grande parte do seu trabalho perdido. Consciente das dificuldades que o paradoxo lhe trazia, Frege acrescentou um apêndice ao livro como resposta a esta descoberta de Russell no qual não pode deixar de expressar uma enorme consternação:
"Um cientista dificilmente se pode deparar com algo tão indesejável como o de ver os fundamentos ruírem exactamente quando o seu trabalho está terminado. Fui colocado nesta posição por uma carta do Sr. Bertrand Russell, quando o trabalho já estava quase todo impresso."
Em resultado do paradoxo, Frege viu-se obrigado a abandonar muitos dos seus pontos de vista. Russell, que entretanto publica "The Principles of Mathematics", acrescenta também ao seu livro um apêndice onde explica em detalhe o paradoxo.
Este paradoxo possui uma versão mais popular intitulada O Paradoxo do Barbeiro.
O paradoxo considera uma aldeia onde um barbeiro faz a barba todos os dias a todos os hoomens que não se barbeiam a si próprios, e a mais ninguém. Ora tal aldeia não pode existir:
- Se o barbeiro não se barbeia a si mesmo, então terá de fazer a barba a si mesmo.
- Se ele se barbear a si mesmo, de acordo com a regra ele não se poderá barbear a si mesmo.
Tuesday, March 28, 2006
Goodbye
Goodbye's the saddest word I'll ever hear
Goodbye's the last time I will hold you near
Someday you'll say that word and I will cry
It'll break my heart to hear you say goodbye
'Till we meet again...
Until then...
Goodbye
Goodbye's the last time I will hold you near
Someday you'll say that word and I will cry
It'll break my heart to hear you say goodbye
'Till we meet again...
Until then...
Goodbye
Sunday, March 26, 2006
Hades
 Hades é o deus do mundo inferior, soberano dos mortos. Embora Hades parecesse sinstro e frio, não era considerado satânico ou maldoso. Era sim, implacavelmente justo e irrevogável em seus decretos, mas nunca foi inimigo da Humanidade e nunca fez mal a ninguém. O seu império é tecido de sombras, frio, trevas e de todas as sensações pertinentes a uma depressão profunda. Hades, assim como Zeus e Poseidon, era retratado como um homem maduro de barba espessa e um olhar severo, muitas vezes com um capacete, presente dos Cíclopes, que possuía o poder da invisibilidade. Já quando era representado como o Deus da riqueza, trazia consigo uma cornucópia ou chifre repleto de iguarias. Quando sentado no seu trono de ébano ou de enxofre, tinha um ceptro negro, uma forquilha ou uma lança. Outras vezes, mostrava uma chave na mão, que simbolizava que as portas da vida estão sempre fechadas àqueles que visitassem o seu império. Também já foi representado numa carruagem conduzida por quatro cavalos negros.
Hades é o deus do mundo inferior, soberano dos mortos. Embora Hades parecesse sinstro e frio, não era considerado satânico ou maldoso. Era sim, implacavelmente justo e irrevogável em seus decretos, mas nunca foi inimigo da Humanidade e nunca fez mal a ninguém. O seu império é tecido de sombras, frio, trevas e de todas as sensações pertinentes a uma depressão profunda. Hades, assim como Zeus e Poseidon, era retratado como um homem maduro de barba espessa e um olhar severo, muitas vezes com um capacete, presente dos Cíclopes, que possuía o poder da invisibilidade. Já quando era representado como o Deus da riqueza, trazia consigo uma cornucópia ou chifre repleto de iguarias. Quando sentado no seu trono de ébano ou de enxofre, tinha um ceptro negro, uma forquilha ou uma lança. Outras vezes, mostrava uma chave na mão, que simbolizava que as portas da vida estão sempre fechadas àqueles que visitassem o seu império. Também já foi representado numa carruagem conduzida por quatro cavalos negros.Saturday, March 25, 2006
Be yourself
"Papa used to say you're just a loser and you're never gonna have what it takes
Mama used to say all that loud music you play ain't gonna get you nowhere
Mama used to say all that loud music you play ain't gonna get you nowhere
You gotta be yourself"
Pensamentos Laterais - Semáforo
E ficou vermelho. O semáforo pregou-me uma partida ao ficar vermelho exactamente naquele momento. O momento em que, num autocarro cheio do que se pode chamar de pessoas, o silêncio imperou. Vi-me confrontado com algo que não pensei que fosse possível. Aquele barulho tao detestável, mas ao mesmo tempo reconfortante, das conversas de autocarro, tinha desaparecido.
Naqueles segundos transformados em horas, eu ouvia os pensamentos assustados do que se pode chamar de pessoas: "será que ele me vai assaltar?", "porque olha tão fixamente para mim?", "devo dar o lugar àquela senhora...não consigo. estou tão bem sentado.", "oh meu Deus, que fui eu fazer. enganei-a!", "será que alguém nota que sou gay?", "odeio estes brancos. quero voltar para Angola.", "hoje não fiz nada de jeito.", "será que ele me viu? espero bem que não. vou fingir que não o vi. não posso com ele...", "como é que a minha família vai sobreviver? não tenho dinheiro.", "estou muito atrasada. e o autocarro que não anda.", "preciso beber. não aguento mais esta solidão."
Mas um som, uma voz mais alta que as outras, aproximava-se tão rapidamente que o embate era inevitável. Mas só então percebi...era de mim que ela saía e sobrepunha-se a todas as outras que agora tão dificilmente se ouviam. E ela dizia-me: "vai embora vermelho! que venha o verde!"
Naqueles segundos transformados em horas, eu ouvia os pensamentos assustados do que se pode chamar de pessoas: "será que ele me vai assaltar?", "porque olha tão fixamente para mim?", "devo dar o lugar àquela senhora...não consigo. estou tão bem sentado.", "oh meu Deus, que fui eu fazer. enganei-a!", "será que alguém nota que sou gay?", "odeio estes brancos. quero voltar para Angola.", "hoje não fiz nada de jeito.", "será que ele me viu? espero bem que não. vou fingir que não o vi. não posso com ele...", "como é que a minha família vai sobreviver? não tenho dinheiro.", "estou muito atrasada. e o autocarro que não anda.", "preciso beber. não aguento mais esta solidão."
Mas um som, uma voz mais alta que as outras, aproximava-se tão rapidamente que o embate era inevitável. Mas só então percebi...era de mim que ela saía e sobrepunha-se a todas as outras que agora tão dificilmente se ouviam. E ela dizia-me: "vai embora vermelho! que venha o verde!"



